R package TSP - Infrastructure for the Traveling Salesperson Problem

Introduction

The TSP package (Hahsler and Hornik 2007) provides the basic infrastructure and some algorithms for the traveling salesman problems (symmetric, asymmetric and Euclidean TSPs). The package provides some fast implementations of simple algorithms including:

• Tour construction heuristics
  • insertion algorithms: nearest insertion, farthest insertion, cheapest insertion, arbitrary insertion (Rosenkrantz, Stearns, and Philip M. Lewis 1977)
  • nearest neighbor methods: Nearest neighbor and repetitive nearest neighbor (Rosenkrantz, Stearns, and Philip M. Lewis 1977)
• Improvement methods
  • two-opt heuristic (Croes 1958)
  • simulated annealing (Kirkpatrick, Gelatt, and Vecchi 1983)
• State-of-the-art solver
  • An interface to the Concorde TSP solver (Applegate et al. 2000, 2006) and its implementation of the Chained-Lin-Kernighan heuristic (Applegate, Cook, and Rohe 2003) is provided (needs to be installed separately).

The package can read and write the TSPLIB format (Reinelt 1991) and it can solve many of the problems in the TSPLIB95 problem library (local copy of the archive).

The following R packages use TSP: archetypes, cholera, condvis, CRTspat, ForagingOrg, ggEDA, isocir, jocre, MLCOPULA, nilde, nlnet, PairViz, pencopulaCond, SCORPIUS, sensitivity, seriation, sfnetworks, tspmeta, VineCopula

To cite package ‘TSP’ in publications use:

Hahsler M, Hornik K (2007). “TSP - Infrastructure for the traveling salesperson problem.” Journal of Statistical Software, 23(2), 1-21. ISSN 1548-7660, doi:10.18637/jss.v023.i02 https://doi.org/10.18637/jss.v023.i02.

@Article{,
  title = {TSP -- {I}nfrastructure for the traveling salesperson problem},
  author = {Michael Hahsler and Kurt Hornik},
  year = {2007},
  journal = {Journal of Statistical Software},
  volume = {23},
  number = {2},
  pages = {1--21},
  doi = {10.18637/jss.v023.i02},
  month = {December},
  issn = {1548-7660},
}

Installation

Stable CRAN version: Install from within R with

install.packages("TSP")

Current development version: Install from r-universe.

install.packages("TSP",
    repos = c("https://mhahsler.r-universe.dev",
              "https://cloud.r-project.org/"))

Usage

Load a data set with 312 cities (USA and Canada) and create a TSP object.

library("TSP")
data("USCA312")

tsp <- TSP(USCA312)
tsp

## object of class 'TSP' 
## 312 cities (distance 'euclidean')

Find a tour using the default heuristic.

tour <- solve_TSP(tsp)
tour

## object of class 'TOUR' 
## result of method 'arbitrary_insertion+two_opt' for 312 cities
## tour length: 41941

Show the first few cities in the tour.

head(tour, n = 10)

## Winston-Salem, NC     Charlotte, NC     Asheville, NC    Greenville, SC 
##               306                54                10               110 
##   Spartanburg, NC       Augusta, GA      Columbia, SC    Charleston, SC 
##               260                14                64                52 
##      Savannah, GA  Jacksonville, FL 
##               250               127

Visualize the complete tour.

library(maps)
data("USCA312_GPS")

plot((USCA312_GPS[, c("long", "lat")]), cex = 0.3)
map("world", col = "gray", add = TRUE)
polygon(USCA312_GPS[, c("long", "lat")][tour, ], border = "red")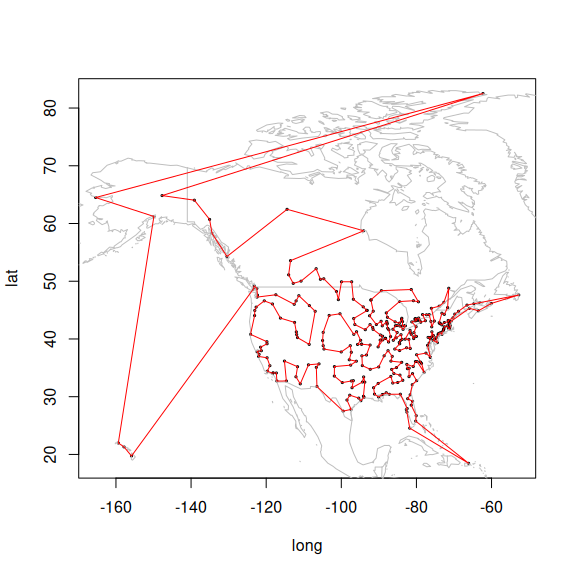

An online example application of TSP can be found on shinyapps.

Help and Bug Reports

You can find Q&A’s and ask your own questions at https://stackoverflow.com/search?q=TSP+R

Please submit bug reports to https://github.com/mhahsler/TSP/issues

References